Contents
수학의 세부 전공을 Combinatorics로 정하게 되면서 Graph theory를 주로 연구했었고 당연히 졸업 논문도 graph structure에 대한 논문을 썼다(궁금하면 여기로). 아무튼 이렇게 달고 살던 graph structure였는데, 딥러닝을 접하면서 소흘해졌었고 GNN의 등장은 알고 있었지만 부족한 개발 실력 탓에 미루고 있었다. 각 분야의 대세 모델을 따라가고 공부하다간 영영 못할 것 같아서 그냥 하고 싶은걸 공부하기로했다.
오늘은 Graph Neural Network를 본격적으로 공부하기 앞서 자주 쓰이는 용어들과 노테이션들에 대해 알아보자.
사실 그래프 구조에는 엄청나게 많은 노테이션이 있지만, “뭘 좋아할지 몰라 다 준비했어” 보다는 공부하면서 등장하는 노테이션들을 차례로 이 글에 업데이트 할 예정이다.
Graph
그래프 G는 set of vertices(혹은 nodes)인 V와 set of edges인 E의 Paired set (V, E)로 표현하는 structure이다. 쉽게 예시를 들어보면
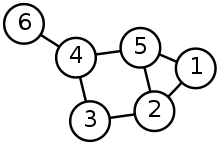위와 같이 생긴 그래프 G가 있다고 하면, 이 그래프의 vertex set V 과 edge set E 는
\(V = \{1,2,3,4,5,6\} \\
E = \{\{4,6\},\{3,4\},\{4,5\},\{2,3\},\{2,5\},\{1,2\},\{1,5\}\}\)
로 표현할 수 있다.
Neighborhood of vertex(node)
그래프의 vertex의 Neighborhood는 해당 점과 이어진, 즉 edge로 연결된 또 다른 vertex를 의미한다. 위 그래프를 다시 예시로 들어보면, vertex “4”의 neighborhood
\(N(4)~or N_4 = \{3,5,6\}\)
으로 표현할 수 있다.
Notation은 통상적으로 Combinatorics에서 사용되는 기호를 기준으로 표현했으며, 사용자에 따라 다르게 표시될 수 있다.
Degree of vertex
어느 한 점 v의 Degree deg(v)는 v가 가지고 있는 edge의 갯수를 의미한다. 당연히 임의의 v에 대하여
\(|deg(v)| = |N(v)|\)
가 됨을 알 수 있다. 하지만 하나의 vertex에서 여러개의 edge가 연결된 multi graph에서는 모든 v에 대해 항상 성립하지 않는다.
Adjacency Matrix(인접행렬)
그래프 \(G = (V, E)\) Adjacency Matrix A의 원소는
\(A_{ij} = \left \{ \begin{array}{cc} 1,~ij\in E\\ 0,~ij\notin E \end{array} \right.\)
로 표현 가능하다. 즉, i-행 j-열에 해당하는 vertex i와 j가 edge로 이어져있으면 1, 그렇지 않으면 0으로 표현하는 행렬이다.
따라서 그래프 의 adjacency matrix는
\(A =
\left (
\begin{array}{cc} 0\\1\\0\\0\\1\\0 \end{array}
\begin{array}{cc} 1\\0\\1\\0\\1\\0 \end{array}
\begin{array}{cc} 0\\1\\0\\1\\0\\0 \end{array}
\begin{array}{cc} 0\\0\\1\\0\\1\\1 \end{array}
\begin{array}{cc} 1\\1\\0\\1\\0\\0 \end{array}
\begin{array}{cc} 0\\0\\0\\1\\0\\0 \end{array}\right)\)
로 표현이 가능하다.
당연하게도 그래프가 멀티그래프 혹은 엣지에 weight가 주어진 경우에는 정의가 달라진다. 지금까지의 내용은 모두 Undirected Graph를 기준으로 한다.