Contents

1. 1. CNN vs GCN
2. 2. Main Idea
3. 3. Notation
4. 4. Graph Convolutional Networks(GCN)
   1. 4.1. Layer-wise propagation rule
5. 5. Graph signal processing
6. 6. Graph Laplacian(Laplacian Matrix)
   1. 6.1. Laplace Operator(라플라스 연산자)
      1. 6.1.1. Laplacian filter in OpenCV
   2. 6.2. Graph Laplacian Operater(Discrete Laplacian for graphs)
   3. 6.3. Normalized Laplacian Matrix
7. 7. Graph Fourier Transform
   1. 7.1. Eigen-decomposition(고유값 분해)
   2. 7.2. (Normalized) Laplacian matrix의 고유값 분해
   3. 7.3. Graph Fourier / Inverse Fourier Transform
8. 8. Summarize

지난 ICLR2017에서 발표된 논문이며, 현재는 5000회가 넘는 인용으로 graph neural network 분야에서 가장 잘 알려진 논문인 Semi-Supervised Classification with Graph Convolutional Networks을 살펴볼 예정이다. 사실 관심있는 분야는 Link Prediction이지만, GNN의 여러 세부 분야 중 가장 잘 알려진 논문으로 맛(?)만 보고 또 지난번 SGAN과 준지도 학습의 범주를 공유한다는 점에서 선택했다.

본 논문의 길이는 사실 짧은 편이지만 이를 이해하기 위해서는 이전의 graph domain에 대한 사전 지식이 많이 필요한데… 아마 내가 수학, 그것도 그래프 이론을 전공하지 않았다면 중간에 읽다가 포기했을 것 같다. 이 내용들을 이해하는 과정에 포커스를 두고 리뷰를 작성하였다.

논문을 읽기 전 graph fourier transform에 대한 사전 지식이 없었기에 이를 먼저 정리하는 차원에서 이번 포스팅을 시작하겠다.

1. CNN vs GCN

Convolutional Neural Network는 이미 너무나도 잘 알려진 방식의 학습 방법이다. Convolution이라는 이름에서 알 수 있듯이 합성곱 연산을 통해 각 레이어마다 weight와 filter의 값들을 스스로 업데이트하며 학습한다. 이는 쉽게말하면 픽셀 값을 업데이트 함을 의미한다.

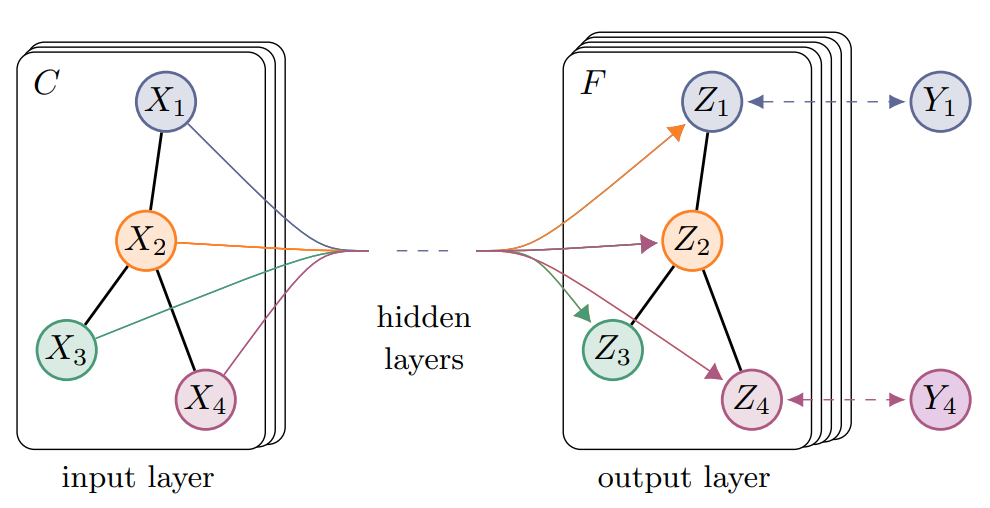
Graph Convolutional Network 역시 마찬가지로 각 레이어를 통과하면서 Convolution 연산을 수행하고 그래프의 어떠한 값을 업데이트 함을 의미한다. 여기서 말하는 ‘어떠한 값’이라는 것은 그래프의 점(vertex)이 될 수도 있고, 선(edge)가 될 수도 있지만, 이번 논문에서는 Vertex의 feature값을 업데이트하는 내용의 논문이다. 무엇을 업데이트하면서 학습하냐에 따라 node classification, link prediction 등으로 나뉘게 된다.

2. Main Idea

그렇다면 Graph Structure에서의 Convolution은 어떻게 정의되고 구현되는 것일까? 논문에서는 크게 3가지에 관해 말하고 있다.

1. 그래프의 각 노드의 feature와 adjacency matrix A가 주어졌을 때, 이를 이용해 classification할 수 있는 multi-layer graph convolutional network(GCN) 즉, \(f(X,A)\)를 제시하였다.

2. 제시한 방법이 빠르고 효율적인(Fast Approximate Convolutions on Graph) 근사임을 증명하였다.

3. 이전의 semi-supervised 연구에서 사용되었던 loss는 “연결된 vertex간에는 유사한 label을 지닌다”고 학습되었기에 graph가 지닌 추가적 정보를 담지 못하는 한계가 존재했다고 한다. 본 논문에서 제시한 GCN은 adjacency matrix를 입력에 사용함으로써 이에 대한 제한을 해결했다고한다.

3. Notation

기본적인 노테이션은 앞서 포스팅했지만, 새로 등장하는 것들이 있기에 다시 알아보기로 한다.

• Graph \(G\), Vertex set \(V\) and Edge set \(E\)

• \[G = (V, E)~ where~v_i\in V~with~size~|V|~and~\{v_i,v_j\}\in E\]

• Adjacency Matrix \(A\)는 \(|V|\times|V|\)차원의 원소 \(A\in \mathbb{R}^{V\times V}\) 이고, 그 원소가

  \[A_{ij} = \left \{ \begin{array}{cc} 1,~ij\in E\\ 0,~ij\notin E \end{array} \right.\]

graph laplacian로 표현되는 adjacency matrix는 vertex label i와 j가 edge로 연결되어 있을 경우 1, 그렇지 않을 경우 0으로 표현되는 matrix이다.

• Degree matrix D

  Degree matrix는 diagonal matrix의 한 종류로, adjacency matrix의 i-th행의 모든 열을 합한 값을 i-th행 i-th열에 넣은 matrix로 표현된다. \(D_{ii} = \sum_jA_{ij}\) 정의는 이러하지만, 직관적으로 살펴보면 말 그대로 vertex들의 각 degree 값을 diagonal로 나타낸 행렬이라 할 수 있다.

4. Graph Convolutional Networks(GCN)

이 논문에서는 새로운 방식의(Graph domain에서의) Convolution rule을 제시한다. 주어진 그래프의 각 vertex의 Feature X와 Adjacency matrix A가 주어질 때, “layer-wise propagation rule” \(f(X,A)\)는 다음과 같다.

4.1. Layer-wise propagation rule

\(l+1\)번째 Hidden state에 대한 식은 아래와 같으며 각 term에 대한 내용은 아래와 같다.

• \(H^{(l)}\): \(l\)번째 layer의 Hidden state를 의미하고, 초기값 \(H^0 = X\)(그래프 노드의 초기 feature)이다.
  • \(\tilde{A}\): \(A + I_N\) 으로, 인접행렬(\(A\))에 자기 자신으로의 연결(\(I_N\))을 추가한 것을 의미한다.
  • \(\tilde{D}\): \(\tilde{D}_{ii} = \sum_{j} \tilde{A}_{ij}\) 로, \(\tilde{A}\)와 동일한 방식으로 자기 자신의 degree까지 추가했다고 생각하면 이해하기 쉽다.
  • \(W^{(l)}\): \(l\)번째 layer의 학습가능한 parameter를 의미한다.
  • \(\sigma\): activation function으로 \(ReLU(\cdot)\)를 사용했다.

이와 같은 Graph convolution 연산을 여러 번(Multi-layer) 진행함으로써 GCN을 구성한다고 말하고 있다. 앞서 인트로에서 CNN과의 간단한 비교와 함께 GCN은 vertex의 feature를 업데이트하는 방식의 Convolution이라고 설명했다. 그렇다면 왜 Graph에서는 기존 Convolution 방식의 적용이 불가능할까?

5. Graph signal processing

전통적인 방식의 Convolution 연산은 \(f * g(x) = \sum_y f(y)g(x-y)\)로 표현되며, \(y\)라는 영역(차원) 내에서 \(g\)라는 filter가 \(f\)와 곱해진 뒤 더해지는 연산이라 볼 수 있다. 하지만, spatial space(공간 영역)에서는 Graph structure에 우리가 알던 convolution 연산은 적용하기 힘들다.

조금 더 얘기하자면, 적분의 형태로 표현되는 기존의 Conolution 계산은 비유클리드 공간 위에 존재하는 Graph structure의 경우 불가능하다. 유클리드 공간의 제5공준인 “평행선 공준”이 만족하지 않기 때문이다. 이 내용은 너무 방대하므로 여기서는 다루지 않는다.

아무튼 이러한 이유로 그래프 구조의 Convolution이 가능한 상태로 만들기 위해 Signal processing분야로부터 확장된 Graph Signal Processing을 사용하는데 이 때 Graph Fourier Transform과 Graph Laplace Transform으로 Graph Signal을 주로 처리한다.

Graph signal

여기서 말하는 graph signal이란 그래프의 vertex 하나에 담겨있는 feature를 의미한다.

6. Graph Laplacian(Laplacian Matrix)

앞에서도 언급했듯이 Graph signal processing 분야는 전통적인 신호처리 분야의 개념을 확장했다고 볼 수 있고, Graph Fourier Transform과 Graph Laplace Transform도 마찬가지이다.

6.1. Laplace Operator(라플라스 연산자)

• 전통적인 Laplace Operator의 경우 그 정의는 다음과 같다.

식을 살펴보면 Laplacian operator(\(\Delta f\))는 벡터함수 \(f\)가 벡터장 내에서 가장 급격히 변하는 정도인 Gradient( \(\nabla f\))에 단위 단면적으로부터 퍼져 나가는 정도를 알려주는 Divergence(\(\nabla\cdot\))를 계산한 것이다. 이는 라플라시안 연산자가 벡터장 내에서 벡터의 흐름이 균일한지 여부를 알려준다고 생각하면 이해하기 쉽다.

6.1.1. Laplacian filter in OpenCV

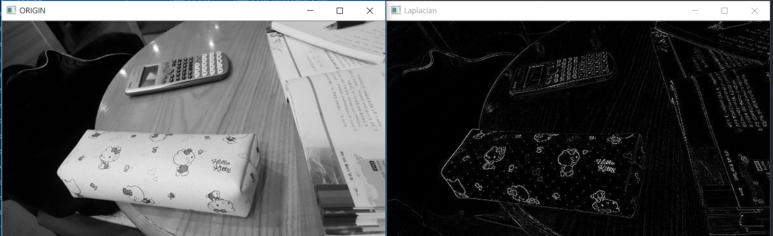
실제로 이미지 처리에서 OpenCV의 Laplace 필터를 활용해 이미지의 외곽선을 검출하는 방식은 외곽에서 라플라스 연산자의 값이 다름을 통해 이를 검출하는 예시가 됨을 확인할 수 있다.

6.2. Graph Laplacian Operater(Discrete Laplacian for graphs)

그렇다면 Graph structure에서의 라플라스 연산자는 어떤 의미를 지니고 있을까? 우선 그 정의는 다음과 같다.

• Let \(G=(V,E)\) be a graph with vertices \(V\) and edges \(E\). Let \(\phi:V\rightarrow R\) be a function of the vertices in a ring. Then, the discrete Laplacian \(\Delta\) acting on \(\phi\) is defined by

• \[(\Delta\phi)(v)=\sum_{w:d(w,v)=1}[\phi(v)-\phi(w)]\]
• where \(d(w,v)\) is the graph distance between vertices \(w\) and \(v\).

여기서 말하는 \(d(w,v)\)는 두 vertex \(w\)와 \(v\)를 잇는 최단 경로에 속하는 edge의 갯수를 의미한다. 어렵게 정의되어 있지만, 함수 \(\phi:V\rightarrow R\)(여기서 Ring \(R\)은 Abstract Algebra에서 정의되는 구조 중 하나이다.)는 그래프의 vertex들에 번호를 붙이는 규칙으로 생각하면 이해하기 쉽다. 이때, 점 \(v\)과 distance=1 거리에 있는 점 \(w\)들을 모아 계산한 것이 Graph Laplacian \((\Delta\phi)(v)\)이 되는 것이다.

• Example)

  

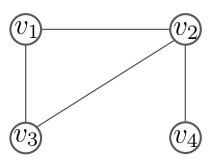
  그래프 \(G\)가 위와 같이 주어졌을 때, Graph Laplacian \((\Delta\phi)(v)\)를 계산해보면 다음과 같다. 먼저 \(v\)가 각 vertex 일 때의 term을 계산해보면 :

  \[\begin{align} v_1 &=\phi(v_1)-\phi(v_2)+\phi(v_1)-\phi(v_3)\\ &= 2\phi(v_1)-\phi(v_2)-\phi(v_3)\\ v_2&=\phi(v_2)-\phi(v_1)+\phi(v_2)-\phi(v_3)+\phi(v_2)-\phi(v_4)\\ &= 3\phi(v_2)-\phi(v_1)-\phi(v_3)-\phi(v_4)\\ v_3&=\phi(v_3)-\phi(v_1)+\phi(v_3)-\phi(v_2)\\ &= 2\phi(v_3)-\phi(v_1)-\phi(v_2)\\ v_4&=\phi(v_4)-\phi(v_2) \end{align}\]

  와 같다. 이 결과를 모두 합한 \((\Delta\phi)(v)\)는 다시 다음과 같이 정리할 수 있다.

이 때, 앞에 곱해진 계수로 이뤄진 행렬이 Graph Laplacian(혹은 Laplacian Matrix) \(L\)이다.

위 예시에서 Graph Laplacian Operater의 정의로부터 Laplacian Matrix를 계산하는 과정은 vertex간의 연결성에 대한 내용임을 눈치챘을 것이다. Graph distance \(d(v,w)=1\)이라는 점이 직접적으로 연결된 vertex들 간의 상호 관계를 의미하고 있기 때문이다. 이 같은 관점에서 전통적 방식의 Laplacian operator와 비교했을 때, 어느정도 일맥상통한 부분을 발견할 수 있다.

Graph \(G=(V,E)\)의 degree matrix를 \(D\), adjacency matrix \(A\)라고 할 때, Laplacian Matrix \(L\)은 \(L = D - A\)로 정의하기도 한다.

6.3. Normalized Laplacian Matrix

위에서 구한 Laplacian matrix는 그래프의 vertex 및 edge들의 사이즈가 커지고 복잡해질수록 그 값이 커지거나 작아지기 때문에(vertex에 연결되어 있는 edge들의 총합이 커지기 때문) 이를 feature embedding의 관점에서 봤을 때, 정규화(normalized)할 필요성이 있다. 본 논문에서 직접적인 언급은 되어있지 않지만, 근사시키는 과정에서 필요하기 때문에 이를 알아보자.

• Normalized laplacian matrix \(\mathscr{L}\)의 정의는 다음과 같다 :

• \[\mathscr{L}:= D^{-\frac{1}{2}}LD^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\]

• 또한, 행렬의 원소 \(\mathscr{L}_{i,j}\)는 다음과 같다.

• \[\mathscr{L}_{i,j}:=\begin{cases} 1 & \mbox{if }i=j\mbox{ and deg}(v_i)\neq 0 \\ -\frac{1}{\sqrt{\mbox{deg}(v_i)\mbox{deg}(v_j)}} & \mbox{if }i\neq j\mbox{ and }v_i\mbox{ is adjacent to }v_j\\ 0 & otherwise \end{cases}\]

로 표현 가능하다. 실제로 계산해보면 Laplacian matrix가 지닌 degree와 adjacency 정보를 정규화시킨 모습으로 나타내짐을 확인할 수 있다. degree 정보가 포함된 주대각 성분들을 모두 1로 만들고, 나머지 adjacency 정보를 degree 수에 맞게 조화평균으로 나눈 모습이다.

7. Graph Fourier Transform

지금까지의 내용은 돌아온 것 같지만 사실 Graph signal을 처리하기 위한, 그 중에서도 Graph Fourier Transform을 사용하여 spatial하지 않은 graph 데이터를 처리하기 위한 준비 과정이다.

7.1. Eigen-decomposition(고유값 분해)

먼저, 더 나아가기 앞서 고유값 분해(Eigen-decomposition)에 대해 알아둘 필요가 있다.

• 행렬 \(A\)는 \(n\times n\)인 정방행렬이며, $n$개의 Linear independent한 eigenvector \(q_i(where~i = 1,\cdots, n)\)를 가졌다고 가정할때, 행렬 \(A\)는 다음과 같이 분해될 수 있다.

• \[A = Q\Lambda Q^{-1}\]

• 여기서 \(Q\)는 \(i\) 번째 열이 \(A\)의 eigenvector \(q_i\) 인 \(n \times n\) 사이즈의 행렬이고, \(\Lambda\)는 고유값 eigenvalue \(\Lambda_{ii} = \lambda_i\)를 대각 원소로 가지는 Diagonal matrix이다. 이때, 대각화 가능한 행렬만이 고유값 분해를 실시할 수 있다.

  위와 같이 특정 조건을 만족하는 행렬 \(A\)에 대해서 고유값 분해가 가능한데, 한 가지 특징을 말하자면 'Symmetric matrix'의 경우는 항상 고유값 분해가 가능하다는 점이다.

  • 즉, \(A\)가 Symmetric matrix일 때, \(Q\)는 \(A\)의 eigenvector를 열벡터로 가지는 직교 행렬(Orthogonal matrix)가 된다
  • 직교행렬 \(Q\)는 \(QQ^\top=Q^\top Q=I(\text{ identity matrix })\)를 만족하는 행렬이다.

7.2. (Normalized) Laplacian matrix의 고유값 분해

그렇다면 갑자기 왜 고유값 분해를 알아봤을까? 눈치 챘겠지만, 우리는 위에서 다룬 Laplacian matrix에 대해 고유값 분해를 진행할 예정이다. 특히, 마지막에 언급했듯이 Symmetric matrix는 항상 고유값 분해가 가능한데 Laplacian matrix \(L\)은 \(L = D-A\)로 정의되는만큼 항상 symmetric하다. 따라서 다음과 같이 표현할 수 있다.

• \[L = U\Lambda U^\top\]
• 여기서 \(U\)는 Laplacian matrix \(L\)의 eigenvector이며 symmetric한 성질을 지녔으므로 \(UU^\top=I\)를 만족한다.

지금까지 우리는 (Normalized) Laplacian matrix (이하 Laplacian matrix)가 eigen-decomposition 가능함을 확인하였고, 이때 분해되는 eigenvector의 직교성(Orthogonal, 우리의 \(L\)은 이미 normalized 하기 때문에 Orthonormal 하다)을 확인하였다.

7.3. Graph Fourier / Inverse Fourier Transform

이를 활용한 Graph Fourier Transform(\(\mathcal{GF}[f]\))을 정의하면 다음과 같다.

• Undirected graph \(G=(V,E)\)가 주어졌을 때, graph signal \(f : V\rightarrow\mathbb{R}\)은 각 점들에서 정의 된 함수이다.

• \(\lambda_l\)과 \(\mu_l\)이 Laplacian matrix \(L\)의 \(l\)번째인 고유값과 고유벡터라고할 때, 그래프 \(G\)의 vertices의 graph signal \(f\)의 Graph Fourier Transform(GFT) \(\hat{f}\)는 다음과 같이 정의된다. 단 Laplacian matrix \(L\)의 고유벡터는 오름차순으로 정렬되어 있다고 가정한다, i.e., \(0= \lambda_{0} \leq \lambda_{1} \leq \cdots \leq \lambda_{N-1}\).

• \[\mathcal{GF}[f](\lambda_l)=\hat{f}(\lambda_l)=\langle f, \mu_l\rangle =\sum_{i=1}^{|V|}f(i)\mu_l^*(i), \text{ where }\mu_l^*=\mu_l^T.\]

• Laplacian matrix \(L\)은 symmetric matrix이므로, 고유벡터 \(\{\mu_l\}_{l=0,\cdots, N-1}\)는 orthogonal basis가 된다. 따라서 Graph의 Inverse Fourier Transform(IGFT)가 존재하고 그 내용은 다음과 같다.

• \[\mathcal{I} \mathcal{G} \mathcal{F}[\hat{f}](i)=f(i)=\sum_{l=0}^{N-1} \hat{f}\left(\lambda_{l}\right) \mu_{l}(i)\]

즉, 앞서 알아본 Laplacian matrix의 \(U^\top\)가 \(U^{-1}\)와 같은 의미를 지닌다는 것을 알 수 있다. 이는 논문의 식 (3)이 왜 Graph Fourier transform으로 표현되는지를 보여준다. Vector \(x\)에 \(U^\top\)를 곱한 뒤 \(g_\theta\)와 연산한 후 다시 \(U\)를 고해 원래 spectral domain으로 돌아오는 방식으로 convolution을 정의한 것이다.

직관적인 의미에서 푸리에 변환은 Input이 되는 임의의 입력 신호를 다양한 주파수로 표현되는 주기함수들의 합으로 분해하여 표현함을 의미한다. Graph convolution의 경우에 학습하기 힘든 vertex feature를 이미 알고있는 푸리에 도메인에서 계산하기 위함이다. (물론 그 과정에서 그래프의 vertex feature 값들을 보다 정밀하게 근사시키는 것이 논문의 목표이다.)

Fourier transform에 대한 더 자세한 내용은 여기서 확인하기 바란다.

8. Summarize

이번 GCN 리뷰(1) 포스팅은 사실 Spectral Graph Convolution을 이해하기 위한 내용이다. 특히, 그림에서 빨간색의 밑줄 친 단 한 줄을 설명하기까지의 내용이다.

\(g_\theta\)가 \(L\)의 고유값으로 생각할 수 있는 이유는 normalized Laplacian matrix의 가운데 끼인 \(g_\theta(\Lambda)\)라고 볼 수 있기 때문이고, 이 \(\Lambda\)가 \(U\)와 \(U^\top\)의 eigenvalue인 이유는 symmetric matrix에서의 고유값 분해를 통해서 가능함을 알아보았다.

특히, Graph convolution((3)번 식)을 정의하기 위해서는 Spatial domain이 아닌 spectral convolution이 필요하며, 이를 위한 graph Fourier transform을 하는 과정에서 \(U^\top\)의 \(U\)가 orthonormal하기 때문에 식 (3)의 연산이 graph convolution으로 정의될 수 있음을 알 수 있었다.

다음 포스팅에서는 이렇게 정의된 convolution을 효율적으로 근사시키는 과정에 대해 알아보며 논문 리뷰를 마치도록 하겠다.