Contents
이번 포스팅은 최근 2년간의 NLP task에서 SOTA를 기록했던 모델들의 모태가 되는 Transformer(NIPS 2017)에 대한 논문을 리뷰하려 한다. Transformer 구조가 특히나 인기(?)를 끌었던 이유중 하나는 논문의 제목도 한 몫을 했다고 생각한다. Attention is all you need이라는 제목에서 짐작할 수 있듯이, 기존까지의 NMT 분야에서 주로 사용되었던 RNN기반의 아키텍쳐가 사용되지 않고, attention 기반의 구조만(그런데 이제 약간 Positional Encoding을 섞은)을 사용한 모델이다.
아무튼 제목 때문에 NLP에 대한 지식이 없었던 나로서는 이 논문이 attention 구조가 등장한 첫 논문이라고 생각했었다. (attention 구조의 첫 등장은 Neural Machine Translation by Jointly Learning to Align and Translate라는 논문이다.)
이전 포스팅에서 리뷰하였으니 attention에 대한 정보가 없다면, 간단히 참고하는 것을 추천한다.
1. Motivation
Transformer는 바로전 리뷰한 논문인 Neural Machine Translation by Jointly Learning to Align and Translate에서의 단점을 보완한 architecture이다. 해당 논문에서는 alignment(이하 attention)을 통해 기존 seq2seq 구조에서 '고정된 길이로 압축되는 context vector'의 단점을 극복했다고 언급했다. 하지만, 여전히 BiLSTM을 이용하며, 이 같은 sequential한 구조는 학습 속도와 긴 문장의 학습에 한계를 가지고 있었다.
논문에서는 attention mechanism에 기반한 transformer라는 모델을 제안하고, 기계 번역 task에서 그간 보여주지 못했던 최고 수준의 결과를 보여주었다.
2. Model Architecture
Transformer는 encoder와 decoder로 이루어져있다. Symbol representations \((x_1, \dots, x_n)\)를 encoder의 input으로 받으면 continuous한 sequence \(\mathbb{z}=(z_1, \dots, z_n)\)로 mapping해주고, 이 \(\mathbb{z}\)는 다시 decoder를 거쳐 \((y_1, \dots, y_m)\)가 생성된다.
각 단계는 auto-regressive(자동회귀)하며, 다음 단계의 symbol 생성시 이전단계의 symbol을 추가 입력으로 받는다.
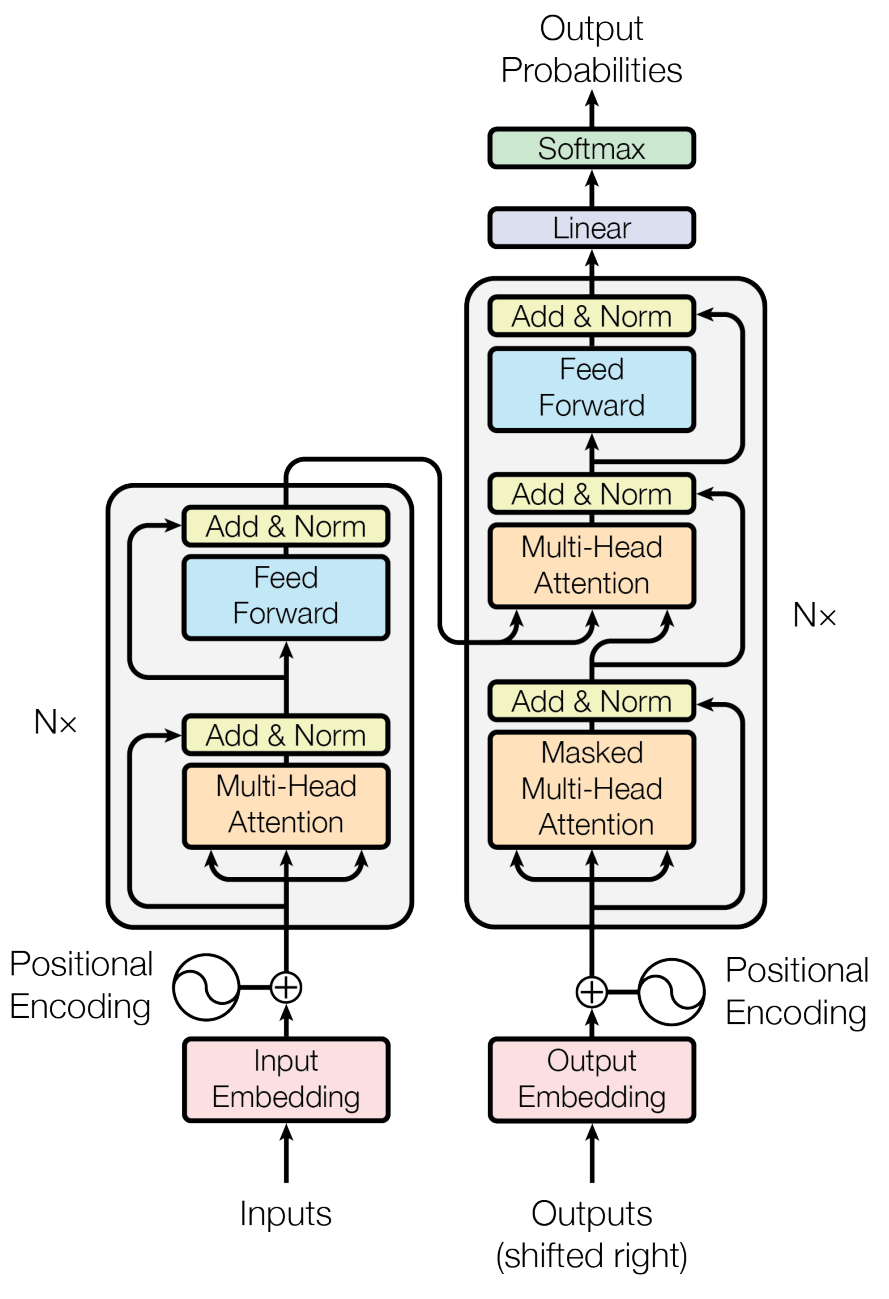
2.1. Encoder and Decoder Stacks
-
Encoder : 위 그림과 같이 인코더는 N=6개의 동일한 레이어 스택으로 구성된다. 각 스택은 두 개의 하위 레이어로 구성되는데,
- multi-head self-attention
- positionwise fully connected feed-forward network
의 두 레이어로 구성되어 있다.
-
Decoder : encoder와 마찬가지로 N=6 개의 동일한 레이어 스택으로 구성되어있다. 단, encoder와 달리 추가적인 layer가 포함되어 있다.
- masked multi-head attention
이는 디코더가 출력을 생성할 시, 다음 출력에서 정보를 얻는 것을 막기 위해 masking을 사용하는 layer이다.
모든 layer는 공통적으로 “Add & Norm” layer를 뒤에 붙이고 있는데, 이는 residual connection으로 구성되어 있다. 각 layer의 input은 x이고 output은 sublayer(x)라고 할 때, 각 layer의 output은 LayerNorm(x + sublayer(x))로 이루어진다. 기존 정보 x를 입력 받으면서, 추가적인 residual 부분만을 받기 때문에 학습 속도가 높고, 초기 모델 수렴 속도가 빠르다.
기본적인 encoder-decoder 구조라는 것을 알았으니 다음 절부터는 좀 더 자세히 인코더와 디코더를 구성하는 layer에 대해 알아보고, 마지막에 작동 원리를 간단히 요약하며 마무리할 예정이다.
2.2. Attention(self-attention)
먼저, transformer에서 가장 핵심이 되는 multi-head attention layer에 대해 알아보도록 하자.
논문에서 어텐션 함수는 Query와 Key-value pair의 관계를 output으로 mapping(함수)한다고 말하고 있다. 즉, Input 값으로 받은 Query와 Key-Value vector를 바탕으로 output을 도출하는 함수이며, 이때 output은 value값의 weighted sum으로 계산된다고 한다.
트랜스포머 구조에서의 attention은 multi-head attention으로 이뤄져있고, 이 multi-head attention은 scaled dot product attention으로 구성되어 있다. 무슨소리냐고? 이제부터 읽어보자
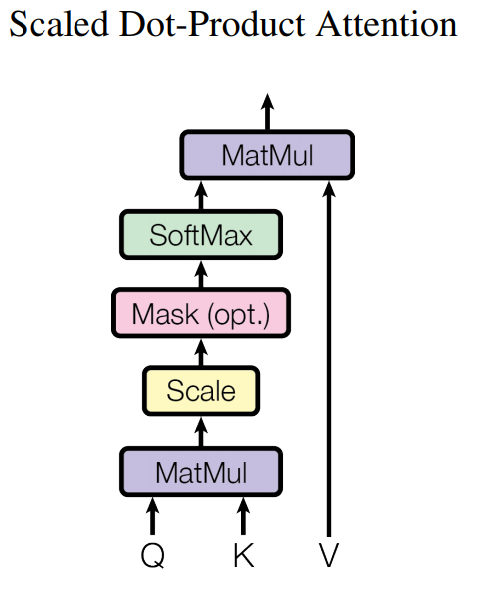
2.2.1. Scaled Dot-Product Attention
Scaled Dot-Product attention layer는 위와 같다.
모든 K(key)로 Q(query)를 내적하고 이를 \(\sqrt d_k\)로 나눠 스케일링한다.
Masking은 패딩된 부분에 대해서는 attention 연산을 하지 않는 과정이며 이는 그림과 같이 옵션이다.
이후 각 벡터를 softmax를 통해 vector에서 token이 갖는 값의 비중을 구하고, 이를 마지막으로 V(value)와 다시 곱하여 attention score를 구한다.
식은 다음과 같다.
\[Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt d_k})V\]논문에서는 attention fucntion은 보통 다음 두 가지를 사용한다고 말한다.
additive attention: 단일 hidden layer의 feed-forward 네트워크를 사용하여 compatibility function를 계산하고, \(d_k\)가 작을 수록 성능이 좋다고 한다.dot-product attention: 반대로 \(d_k\)가 클수록 더 빠르고 효율적인 연산이 가능하다고 한다.
한편, 그림에서 보듯 optional하게 masking layer를 사용해야 하는 경우가 있다. 이는 아래 multi-head attention의 마지막 부분에서 설명하도록 한다.
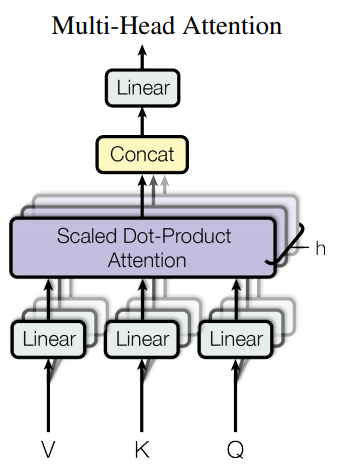
2.2.2. Multi-Head Attention
Multi-Head Attention은 앞서 설명했던 attention 연산을 여러번 수행하는 거라 생각하면 된다.
위의 그림을 살펴보면 앞선 절에서 설명했던 Scaled Dot-Product Attention 연산이 \(h\)번 합쳐진 모습을 볼 수있다.
논문에서는 \(d_{model}\) 차원의 key, value, query들을 사용하는 것보다, 서로 다르게 학습된 linear projection을 사용하여 \(d_k\), \(d_v\), \(d_q\) 각각의 차원으로 h 번 학습시키는 것이 낫다고 한다. 이 때, 단순히 \(h\)번의 횟수는 sublayer의 같은 부분이 \(h\)개 존재함을 의미한다. 이렇게 통과한 \(h\)쌍의 \(d_v\)차원의 출력은 Concatenate되어 출력된다.
다시 돌아와서 단어(token)부터 layer를 통과하기까지를 그림으로 살펴보자.
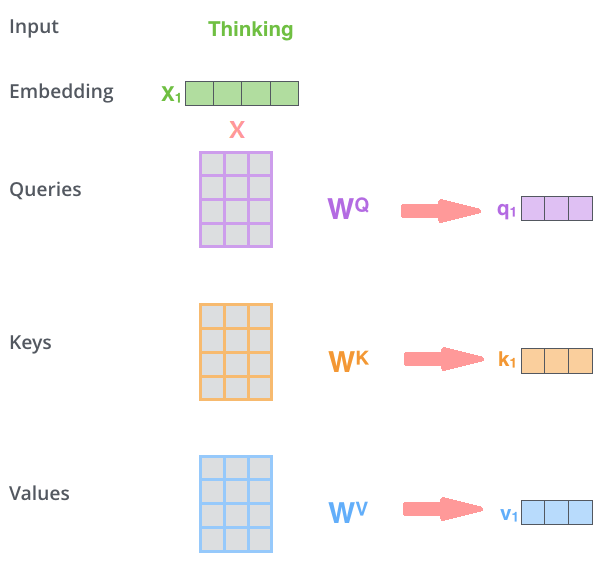
image reference : http://jalammar.github.io/illustrated-transformer/
위 그림처럼 우선 토크나이징 된 “Thinking”이라는 단어를 \(X_1\)라는 vertor로 임베딩을 했다고 가정하자(실제 transformer의 input은 토큰들의 embedding vector가 합쳐진 형태의 embedding matrix로 들어가게 된다). 임베딩 벡터 \(X_1\)에 \(W^Q\), \(W^K\), \(W^V\)라는 가중치 행렬을 곱해 \(q_1\), \(k_1\), \(v_1\) 를 얻는다.
가중치 행렬의 차원은 \(W_i^{Q, K, V}=\mathbb{R}^{d_{model}\times d_k}\)로 만든다. 이 때, \(d_k\)는 \(d_{model}\)을 \(h\)로 나눈 값이다. 그 이유는 multi-head attention의 마지막에 \(h\)개의 attention layer를 concatenate하기 때문이다.
논문에서는 \(h=8\)의 attention layer를 사용하였고, 임베딩 차원은 512 차원으로 사용했다고한다.
이렇게 완성된 각각의 \(q_1\), \(k_1\), \(v_1\)는 Dot-Product attention 연산을 통해 \(z_1\)로 출력된다. 하지만 앞서 말했듯이, Transformer의 input은 문장의 embedding vector를 모두 합친 embedding matrix 형태로 들어가게된다. 따라서 attention연산은 아래와 같이 \(q_1, \dots, q_n\)을 합친 \(Q\), \(k_1, \dots, k_n\)을 합친 \(K\), \(v_1, \dots, v_n\)을 합친 \(V\)의 형태를 거쳐 \(Z\)로 출력된다.
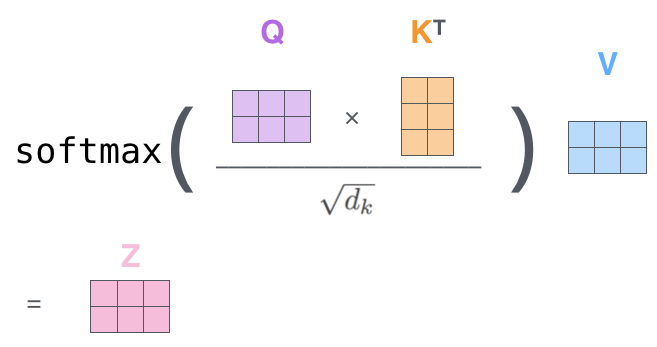
image reference : http://jalammar.github.io/illustrated-transformer/
이렇게 완성된 하나의 \(Z\)는 multi-head attention의 \(h\)개 중 하나의 output이며, 이러한 attention 연상이 총 8번(논문 기준) 수행된다. 여기서 각 attention head에서 만들어진 가중치 행렬 \(W^Q\), \(W^K\), \(W^V\)은 중복되지 않고, 각 head마다 새롭게 계산된다.
이렇게 head마다 계산된 뒤 concatenate된 \(Z_0, \dots, Z_7\)은 마지막 추가 웨이트를 통해 \(Z\)로 출력된다.
논문에서는 총 세 가지 종류의 Attention Layer를 사용한다.
- Encoder Self-Attention
- Masked Decoder Self-Attention
- Encoder-Decoder Attention
Encoder Self-Attention
앞서 설명한 내용을 기본으로 생각하면 이해하기 쉽다. 문장의 단어들이 앞 뒤의 단어들과 self-attention 연산을 수행하면서 attention score를 계산하는 과정이다.
Masked Decoder Self-Attention
Decoder의 첫번째 input이 들어온 뒤의 multi-head attention layer로써, 출력 단어가 자기보다 앞서 이미 앞에 나왔던 단어들만 참고해서 연산하는 attention layer이다. 뒤쪽에 나온 단어까지 참고해 앞을 예측하게 한다면 이는 일종의 cheating처럼 작용해 auto-regressive를 수행하지 못하는 모델이 된다.
이를 위해서는 현재 진행중인 단어보다 뒤쪽 단어들에 대한 masking 작업이 필요하다. Masking의 방식은 아래와 같다.
| query/key | I | am | a | boy |
|---|---|---|---|---|
| I | 23 | \(-\infty\) | \(-\infty\) | \(-\infty\) |
| am | 15 | 27 | \(-\infty\) | \(-\infty\) |
| a | 14 | 20 | 23 | \(-\infty\) |
| boy | 11 | 18 | 22 | 25 |
\(Q\times K^T\)를 통해 만들어진 행렬을 위와 같이 참고하지 않을 부분을 \(-\infty\)로 할당해 줌으로써 softmax의 output이 0으로 수렴하게 만든다.
Encoder-Decoder Attention
Decoder 파트의 두 번째 multi-head attention layer로써, Query는 decoder에 있고, 각각의 Key와 value는 Encoder에 있는 attention 파트이다. “난 널 좋아해”라는 문장을 “I like you”로 번역할 때, “like”라는 단어가 “난”, “널”, “좋아해” 중에서 어떤 단어에 더 많은 가중치를 두는지를 참조하는 과정이다.
Self-Attention
모든 Encoder와 Decoder에서 사용된다. 학습하고자 하는 문장에서 각 단어에 대해 해당 단어가 포함된 자기 자신의 문장의 어떤 단어와 얼만큼 연관있는지를 계산하는 방식을 의미한다.
정형데이터의 상관관계 heatmap을 생각하면 이해하기 쉽다.
2.3. positional encoding
인코딩 및 디코더의 입력값마다 상대적인 위치정보를 더해주는 방법이다. Transformer는 RNN이나 CNN을 사용하지 않는만큼 input word의 순서를 알려주는 layer를 포함하지 않는다. 따라서 input 단어들의 순서를 알려주는 구조가 필요하다.
Positional encoding은 다음과 같은 주기 함수를 사용하여 각 단어의 상대적 위치정보를 학습할 수 있게 도와준다.
\[PE_{(pos, 2i)} = sin(pos /10000^{2i/d_{model}})\\ PE_{(pos, 2i+1)} = cos(pos /10000^{2i/d_{model}})\]여기서 \(pos\)는 각각의 단어 번호(문장 내 단어의 순서)를 의미하고, \(i\)는 각 단어의 임베딩 값의 위치를 의미한다. 이렇게 구한 PE는 input으로 들어온 임베딩 행렬과 element-wise로 더해져서 사용된다.
- 예를 들어 “I am a boy”라는 문장을 512차원의 vector로 임베딩한다고 가정하자. 각 단어는 512차원의 길이를 가지는 vector가 되고, 전체 문장은 4 X 512의 matrix로 임베딩 되어 input으로 들어갈 것이다. 이때, Positional Encoding(PE)역시 4 X 512 크기의 matrix로 구해지게 된다.
- 워드 임베딩 행렬과 PE 행렬은 각각의 자리를 더해 최종적으로 4 X 512 임베딩으로 transformer에 사용된다.
Positional encoding에 사용되는 함수는 꼭 주기함수가 될 필요는 없고, 단지 상대적 위치 정보가 기록될 수 있는 함수면 상관없다. 실제로 이후 발표되는 모델들에 sin, cos함수가 사용되지 않는 경우도 많다.
논문에서는 주기함수를 사용함으로써 학습 데이터보다 더 긴 문장이 들어오더라도 인코딩 값을 할당할 수 있다는 점을 장점으로 말하고 있다.
2.4. Position-wise Feed-Forward Networks
encoder와 decoder 각 파트의 마지막 attention sub-layers에는 FC feed forward network가 포함되어있다. 이는 각 위치마다 개별적으로 동작한다. 여기서는 ReLU가 포함된 두 개의 선형 변환으로 구성된다.
\[\text{FFN(x)} = max(0, xW_1 + b_1)W_2 + b_2\]이 선형 변환은 다른 위치에서 동일하지만, 각 레이어에서 다른 파라미터를 사용한다. 앞서 언급했듯 논문에서는 \(d_{model}=512\)로 사용했고, \(d_{ff}=2048\)를 사용했다.
3. Why Self-Attention?
논문에서는 \((x_1, \dots, x_n)\rightarrow(z_1,\dots,z_n)\)의 mapping에 self-attention이 적합한 이유를 기존의 recurrence 모델 및 convolutional 모델과 비교하여 말하고 있다. 간단하게 요약하자면 다음 표로 나타낼 수 있다.

논문에서는 \(n\)이 짧을 때는 비슷하기 때문에 가장 긴 길이일 때를 비교하였다. 최대 길이가 길 때 long-term dependency가 self-attention에서 매우 낮은 것을 확인할 수 있다. Layer당 계산량이 현저히 작으며, recurrent 모델과는 다르게 병렬화가 가능하다. 기존 RNN 모델의 경우에는 모델이 word의 순서에 맞게 계산해야 했기 때문에 계산 병렬화가 불가능했지만, transformer는 positional encoding으로 이를 극복하였다.
4. Experiments
Transformer 모델은 논문에서 볼 수있듯이 기본 base model로도 엄청난 성능을 보여주고 있다. 특히, Big model의 경우 SOTA를 경신하는 모습을 보여줬다. 더 자세한 실험 결과 및 성능은 직접 논문을 참고하는 것을 추천한다.